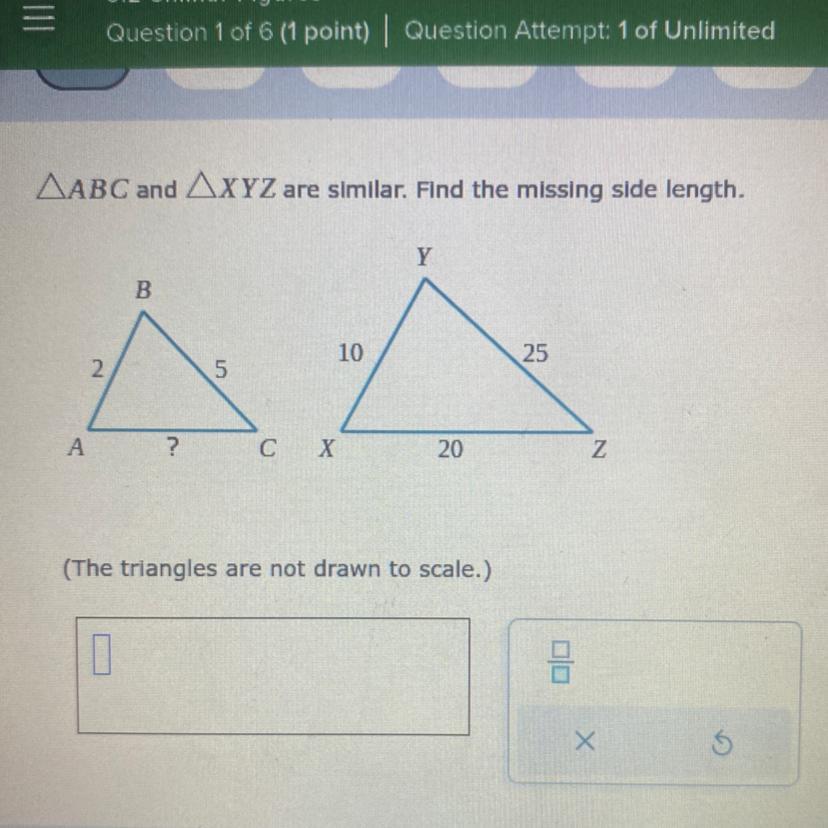
ABC and XYZ are similar. Find the missing side length.

There are no solutions for z³ = x³ + y³ for a right triangle

The equation is given as:

z³ = x³ + y³

By Pythagoras theorem, we have:

z² = x² + y²

Multiply both sides by z

z³ = zx² + zy²

By comparing z³ = zx² + zy² and z³ = x³ + y³, we have:

x³ + y³ = zx² + zy²

Factor out z

x³ + y³ = z(x² + y²)

Make z the subject

z = (x³ + y³)/(x² + y²)

There exist no solution for the above equation

Hence, there are no solutions for z³ = x³ + y³ for a right triangle

Read more about right triangle at:

https://brainly.com/question/2437195

#SPJ1

The following integer values of x satisfy the given inequality,

4, 5, 6, 7, 8

What is an inequality?

An inequality in mathematics is a relation that compares two numbers or other mathematical expressions in an unequal way. The majority of the time, size comparisons between two numbers on the number line are made using inequality.

Solving the Inequality

The given inequality is,

5x + 4 > 19

5x > 19 - 4

5x > 15

x > 15/5

x > 3

So, the required values of x must be greater than 3 in the given interval, [2,8]

Thus, the integer values of x in the the interval [2,8] that satisfy the given inequality are 4, 5, 6, 7 and 8 (∵ Square brackets of an interval denote inclusion of the terminal values).

Learn more about inequality here:

https://brainly.com/question/20383699

#SPJ4

The two cars lying on one side of the plane are 50 meters apart.

An equation is an expression that shows the relationship between two or more numbers and variables.

let us assume that the height is 100 m. Let d represent the horizontal distance. For depression of 38°, Ф = 90 - 38 = 52°, hence:

tan(52°) = d / 100

d = 128 m

For depression of 52°, Ф = 90 - 52 = 38°, hence:

tan(38°) = d / 100

d = 78 m

Distance apart = 128 - 78 = 50 m.

The two cars lying on one side of the plane are 50 meters apart.

Find out more on equation at: https://brainly.com/question/2972832

#SPJ1

the actual height of the backboard is 8.18 feet.

A proportion is an equation that sets two ratios at the same value. For instance, you could express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls)

Given

We have been given that Derek places  a standard 12-inch ruler next to the goal post and measures the shadow of the ruler and the backboard. If the ruler has a shadow of 10 inches. We are asked t find the height of the backboard, if the backboard has a shadow of 8.5 feet.

We will use proportions to solve our given problem as ratio between sides ruler will be equal to ratio of sides of background.

[tex]\frac{Actual height of ruler}{Shadow of ruler} = \frac{Actual height of black board}{Shadow of black board} \\\\\frac{12}{11} =\frac{Actual height of black board}{7.5} \\\\Actual height of black board = \frac{12}{11} * 7.5 = 8.18\\[/tex]

Therefore, the actual height of the back-board is 8.18 feet.

to learn more about proportion refer to:

https://brainly.com/question/1496357

#SPJ9

Answer:

  f(2) = -13

Step-by-step explanation:

Evaluate the given formula with the given value of the variable.

  f(1) = -16 . . . . . . . . . . given

  f(n) = -29 -f(n-1) . . . . given

For n = 2, we have ...

  f(2) = -29 -f(2-1) = -29 -f(1) = -29 -(-16) . . . . put 2 in place of n and evaluate

  f(2) = -13

Answer:

(x + 6)(x - 2) = x² + 4x - 12

(x + 2)(x - 8) = x² - 6x - 16

(x + 6)(x - 6) = x² - 36

(x - 5)(x - 1) = x² - 6x + 5

(x - 4)(x - 10) = x² - 14x + 40

(x + 2)(x + 5) = x² + 7x + 10

Step-by-step explanation:

Use FOIL.

(x + 6)(x - 2) =

F - first: x × x = x²

O - outer: -2 × x = -2x

I - inner: 6 × x = 6x

L - last: 6 × -2 = -12

(x + 6)(x - 2) = x² - 2x + 6x - 12

Now, combine like terms.

(x + 6)(x - 2) = x² + 4x - 12

(x + 2)(x - 8) = x² - 6x - 16

(x + 6)(x - 6) = x² - 36

(x - 5)(x - 1) = x² - 6x + 5

(x - 4)(x - 10) = x² - 14x + 40

(x + 2)(x + 5) = x² + 7x + 10

The graph that shows the minimum amount due for a credit amount of x given that the credit limit is $2,000 is graph B.

Let x represent the credit amount  and y represent the minimum amount due.

For a bill of less than $100, the entire amount is due. That is for 0 ≤ x < $100, y = x

For a bill of at least $100 but less than $500, the minimum due is $100. That is for $100 ≤ x < $500, y = 100

For a bill of at least $500 but less than $1,000, the minimum due is $300. That is for $500 ≤ x < $1000, y = $300

For a bill of $1,000 or more, the minimum due is $500. But the credit limit is $2000. That is For $1000 ≤ x < $2000, y = $500

The graph that shows the minimum amount due for a credit amount of x  is graph B.

Learn more about graph on:

https://brainly.com/question/19040584

#SPJ1

The relationship between the natural variation and specifications is quantified by a measure known as the Process capability index.

According to the questions,

The relationship between the natural variation and specifications is quantified by a measure known as the Process capability index.

Process capability index refers to the capability of a process to deliver output which lies within the specifications limits that are desired.

Hence, the relationship between the natural variation and specifications is quantified by a measure known as the Process capability index.

Learn more about Process capability index https://brainly.com/question/24322347

#SPJ4

A)  Rotate by 90° counterclockwise.

B) Reflection transformation about the line y = 5.

C) Parallel Lines are C₂D₂ and A₂B₂; EF and E₁F₁.

D) Perpendicular lines are;  D₁F₁ and  E₁F₁; DF and EF; DC and AB.

E) Line segments with slope of 0 are; AB, C₂D₂, A₂B₂, EF and E₁F₁

F) Line segments on the boat that have an undefined slope are; Lines A₁B₁, DF and DC.

G) Slope of Line ED = 1

A) The blue segment CD is seen on the graph as a perpendicular line with 2 units while the line segment C₂D₂ is seen as a horizontal line. Thus, to match CD with C₂D₂, we will rotate by 90° counterclockwise.

B) The transformations that would be used on the blue triangle to get it to match with the red triangle is a reflection transformation about the line y = 5.

C) The line segments that are parallel to each other are; C₂D₂ and A₂B₂; EF and E₁F₁.

D) The line segments that are perpendicular are;  D₁F₁ and  E₁F₁; DF and EF; DC and AB.

E) Horizontal lines that are parallel to the x-axis have zero slope. Thus, AB, C₂D₂, A₂B₂, EF and E₁F₁ all have zero slopes.

F) Undefined slope is the slope of a vertical line. Thus, Lines A₁B₁, DF and DC have undefined slopes.

G) Slope of ED = (5 - 4)/(-10 - (-11))

Slope of ED = 1/1

Slope = 1

Read more about Transformations at; brainly.com/question/4289712

#SPJ1

The systems of linear equations have been matched with their respective solutions as shown in the image attached below.

A system of linear equations can be defined as an algebraic equation of the first order that has two (2) variables with each of its term having an exponent of one (1).

In this exercise, you're required to match the systems of linear equations with their respective solutions as shown in the image attached below.

Read more on linear equations here: https://brainly.com/question/2030026

#SPJ1

Using it's formula, the area of the right triangle is of 750 inches squared.

The area of a right triangle is given by half the multiplication of the two legs, which are the two smaller sides.

In this problem, the two legs are 25 inches and 60 inches, hence the area of the triangle is:

A = 0.5 x 25 x 60 = 750 inches².

More can be learned about the area of a triangle at https://brainly.com/question/17335144

#SPJ1

Answer:

r = -1.5

Step-by-step explanation:

recall that ,the recursive formula for a geometric sequence [tex]a_n[/tex] is :

[tex]a_{n} = r \times a_{n-1} \ \ \text{where r is the common ratio }[/tex]

therefore

The common ratio of the sequence:

[tex]a_{n} = -1.5 \times a_{n-1}[/tex]

is r = -1.5

The area of the rectangle is 105 square cm

Represent the dimensions of the rectangle with x and y

So, the length of the square would be:

Length = x - 2

Width = y + 6

The areas are then calculated as:

Rectangle = xy

Square = (x -2)(y + 6)

The relationship between the areas is:

(x -2)(y + 6) = 64 + xy

Expand

xy + 6x - 2y - 12 = 64 + xy

This gives

6x - 2y - 12 = 64

Add 12 to both sides

6x - 2y= 76

Divide through by 2

3x - y = 38

By trial by error, we have:

x = 15 and y = 7

The rectangle area is then calculated as:

Rectangle = xy

This gives

Rectangle = 15 * 7

Evaluate

Rectangle = 105

Hence, the area of the rectangle is 105 square cm

Read more about areas at:

https://brainly.com/question/27683633

#SPJ1

If you register a 0. 08 bac or refuse to take a breath test, your license will be automatically suspended for 12 months.

The amount of alcohol in your blood is determined via a blood alcohol(bac)test. The breathalyzer test, which police officers frequently administer to people they suspect of driving while intoxicated, is more widely known. While breathalyzers provide quick findings, they are not as precise as bac tests that measure alcohol in the blood.

The same 0.08 bac limit applies to adults in all 50 states who are 21 years of age or older, who are driving while intoxicated and breaching the law.

No amount of alcohol is safe when you are driving, even if your bac is below the legal limit. Don't drive after drinking, please!

Learn more about bac test here:

https://brainly.com/question/1307524

#SPJ4

Answer: B

The main word that gives the answer away is product, which means to multiply.

There were 4 number of treatment conditions compared in this experiment for the given degree of freedom.

We have,

df = 3, 36

Now,

We know that,

Degree of freedom (df) = Number of treatments (t) - 1

i.e.

df = t - 1

So,

We have,

df = 3

Now,

Substituting the values,

We get,

3 = t - 1,

i.e.

t = 4

So, number of treatments conditions = 4

Hence we can say that there were 4 number of treatment conditions compared in this experiment for the given degree of freedom.

Learn more about treatments conditions here

https://brainly.com/question/23851035

#SPJ4

Using proportions, it is found that the angular velocity at the tip of the blade is of 753.98 radians per minute.

A proportion is a fraction of a total amount, and the measures are related using a rule of three.

Each revolution has [tex]2\pi[/tex] radians, hence in one minute, the 120 revolutions will have a measure in radians of:

M = 120 x 2pi = 240pi = 753.98

Hence the angular velocity is of 753.98 radians per minute.

More can be learned about proportions at https://brainly.com/question/24372153

#SPJ1

A ratio is a mathematical expression that's used to denote the proportion of two (2) or more quantities with respect to one another and the total quantities.

In Mathematics, a fraction comprises two (2) main parts and these include:

3 to 2 = 3/2

5:6 = 5/6

8 to 12 = 3/2

Thus, a common denominator of 12 can be used to rewrite the fractions and then you should compare the numerators to order the ratios in an ascending order.

Read more on ratio here: brainly.com/question/13513438

#SPJ1

Step-by-step explanation:

well there is a very simple point that you have mistaken tho:

484cm², 25cm²

Areas are defined in square cm but the radius is in cm

so:

[tex] \sqrt{ \frac{484 {cm}^{2} }{25 {cm}^{2} } } = \frac{7.92}{r} = = = > 4.4 = \frac{7.92cm}{x} = = > x = \frac{7.92cm}{4.4} = x = 1.8cm[/tex]

and there you go

Answer:

center (2, 9); radius 6

Step-by-step explanation:

Standard equation of a circle:

(x - h)² + (y - k)² = r²

where the center is (h, k), and r is the radius.

You have

(x - 2)² + (y - 9)² = 36

(x - 2)² + (y - 9)² = 6²

Compare this last form to

(x - h)² + (y - k)² = r²

h = 2; k = 9; r = 9

Answer: center (2, 9); radius 6

Answer:

centre = (2, 9 ) , radius = 6

Step-by-step explanation:

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k ) are the coordinates of the centre and r is the radius

(x - 2)² + (y = 9)² = 36 ← is in standard form

with centre (2, 9 ) and r² = 36 ⇒ r = [tex]\sqrt{36}[/tex] = 6

Point A is at A(2, 3) while point B is 4 right and 5 up from point A. Point B is at  B(6, 8). Also, point C is at C(9, 7). Point D is 8 left and 2 down from point C  which is at D(1, 5).

An equation is an expression that shows the relationship between two or more variables and numbers.

Point A is at A(2, 3) while point B is 4 right and 5 up from point A. Point B is at  B(6, 8). Also, point C is at C(9, 7). Point D is 8 left and 2 down from point C  which is at D(1, 5).

The location of point A, B, C and D is located on the graph.

Find out more on equation at: https://brainly.com/question/2972832

#SPJ1

Answer: 47°

Step-by-step explanation:

Answer:  0.6

Explanation:   You need to divide 3 by 5 and it will give you the answer of 0.6

The right triangle whose hypotenuse is the square root of 17 has legs of 1 inch and 4 inches

Step 1 and 2: Create an isosceles right triangle

This is represented by the attached figure in (see figure 1 for this triangle)

The legs of this triangle have a length of 1 inch

Step 3: The hypotenuse

This is calculated using the following Pythagoras theorem

[tex]h^2 = 1^2 + 1^2[/tex]

This gives

[tex]h = \sqrt 2[/tex]

Step 4: Create another isosceles right triangle

This is represented by the attached figure in (see figure 2 for this triangle)

The legs of this triangle are 1 inch and 2 inches, respectively

This hypotenuse is calculated by:

[tex]h^2 = 2^2 + 1^2[/tex]

This gives

[tex]h = \sqrt 5[/tex]

Step 5: Create another isosceles right triangle

This is represented by the attached figure in (see figure 3 for this triangle)

The legs of this triangle are 1 inch and 3 inches, respectively

This hypotenuse is calculated by:

[tex]h^2 = 3^2 + 1^2[/tex]

This gives

[tex]h = \sqrt {10[/tex]

Step 6: Create another isosceles right triangle

This is represented by the attached figure in (see figure 4 for this triangle)

The legs of this triangle are 1 inch and 4 inches, respectively

This hypotenuse is calculated by:

[tex]h^2 = 4^2 + 1^2[/tex]

This gives

[tex]h = \sqrt{[17[/tex]

See that the hypotenuse is the square root of 17

Hence, the right triangle whose hypotenuse is the square root of 17 has legs of 1 inch and 4 inches

Read more about right triangles at:

https://brainly.com/question/2437195

#SPJ1

Answer:

23

Step-by-step explanation:

  In arithmetic sequence, the difference between any consecutive terms is constant and the progression goes either in  ascending order or in descending order.

a = first term = 2

a₂ = 5

difference = d = second term - first term

                        = 5 - 2

                      d = 3

Formula for finding nth term in arithmetic sequence:

   [tex]\sf \boxed{t_n = a + (n-1)*d}[/tex]

     t₈ = 2 + (8 -1) * 3

        = 2 + 7 *3

        = 2 + 21

    t₈ = 23

Using it's concept, the probabilities are given as follows:

a) 0.5455 = 54.55%.

b) 0.5909 = 59.09%.

c) 0.4615 = 46.15%.

d) 0.5556 = 55.56%.

A probability is given by the number of desired outcomes divided by the number of total outcomes.

Item a:

Out of 110 people, 60 prefer sprite, hence the probability is:

p = 60/110 = 0.5455 = 54.55%.

Item b:

Out of 110 people, 65 are between 21 and 40, hence the probability is:

p = 65/110 = 0.5909 = 59.09%.

Item c:

65 people are between 21 and 40, and of those, 30 drink lemonade, hence the probability is:

p = 30/65 = 0.4615 = 46.15%.

Item d:

45 people are under 21 years of age, and of those, 25 drink sprite, hence the probability is:

p = 25/45 = 0.5556 = 55.56%.

More can be learned about probabilities at https://brainly.com/question/14398287

#SPJ1

Answer:

ABC is congruent to DEF

Step-by-step explanation:

I think its this one cause the angles are the same

The different ratios are 2 : 7, 2 : 9 and 7 : 9

The statement is given as:

8 out of 36 squares unfilled

This means that:

The part-to-part ratio is represented as:

Ratio = Unfilled : Filled

This gives

Unfilled : Filled = 8 : 28

Simplify

Unfilled : Filled = 2 : 7

The part-to-whole ratios are represented as:

Ratio = Unfilled : Total

Ratio = Filled : Total

So, we have:

Unfilled : Total = 8 : 36

Filled : Total = 28 : 36

Simplify

Unfilled : Total = 2 : 9

Filled : Total = 7 : 9

Hence, the different ratios are 2 : 7, 2 : 9 and 7 : 9

Read more about ratio at:

https://brainly.com/question/2328454

#SPJ1

The equilibrium level if autonomous expenditures are $2,000 and the mpe is 0. 5 is $4000.

From the information given, the autonomous expenditures are $2,000 and the mpe is 0. 5.

Here, the equilibrium level will be:

= 2000/(1 - 0.5)

= 2000/0.5

= 4000

In conclusion, the correct option is $4000.

Learn more about expenditure on:

brainly.com/question/935872

#SPJ1

Answer: B

Step-by-step explanation:

Using the distance formula, we get the height is [tex]4\sqrt{2}[/tex].

Similarly, we get the base is [tex]6\sqrt{2}[/tex].

So, the area is [tex]\frac{1}{2}(4\sqrt{2})(6\sqrt{2})=24[/tex]