Answers
Answer:
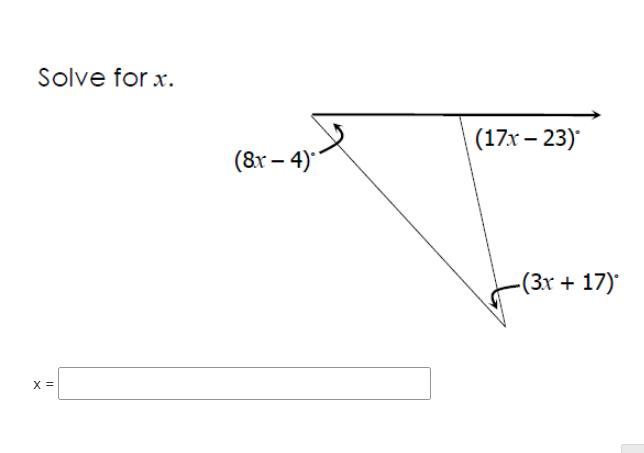
x = 6
Step-by-step explanation:
(8x - 4)° + (3x + 17)° = (17x - 23)° => exterior angle theorem
Solve for x
8x - 4 + 3x + 17 = 17x - 23
Add like terms
11x + 13 = 17x - 23
11x - 17x = -13 - 23
-6x = -36
Divide both sides by -6
x = 6
Related Questions
A recipe for 12 scones requires 2 teaspoons of baking powder and 240 g of flour. If a larger number of scones are made, using 540 g of flour, how much baking powder is needed?
Answers
Answer:
45 teaspoons of baking powder
Step-by-step explanation:
Let x = amt of baking powder needed.
2/240 = x/540
240x = 1080
x = 45 teaspoons of baking powder
find the measure of each angle indicated
Answers
Answer:
D) 111
Step-by-step explanation:
Internal Alternate angle thm states 111 and x are equal:
? = 111
Answer:
D
Step-by-step explanation:
its the same as the angle that was given to you
07:5
Which pair of angles must be supplementary?
VX
2.
6
3
4
5
21 and 26
22 and 25
0 25 and 24
Z6 and 22
Answers
Answer:
∠1 and ∠6
Step-by-step explanation:
Supplementary angles are two or more angles added together make 90°.
Right angles indicated by the small square at the corners.
∠2 and ∠5 are right angles.
So, any pair with ∠2 and ∠5 are not supplementary.
The only pair of angles that are not associated with ∠2 and ∠5 is: ∠1 and ∠6.
Simplify.
2x + 6x2
10 + 4x2 – 3x + (-6) =
Answers
Answer: 14x,4+4x ^2-3x
Step-by-step explanation:
1. Simplify 6x\times 26x×2 to 12x12x.
2x+12x,10+4{x}^{2}-3x-6
2x+12x,10+4x
2
−3x−6
2 Simplify 2x+12x2x+12x to 14x14x.
14x,10+4{x}^{2}-3x-6
14x,10+4x
2
−3x−6
3 Collect like terms.
14x,((10-6)+4{x}^{2}-3x)
14x,((10−6)+4x
2
−3x)
4 Simplify (10-6)+4{x}^{2}-3x(10−6)+4x
2
−3x to 4+4{x}^{2}-3x4+4x
2
−3x) Hope that helps
can somebody help me?
Answers
25 divided by 12 PLEASE answer quick
Answers
24 divided by 12 equals 2,083
The division of 25 by 12 gives the quotient 2 and remainder is 1.
What is Division?One of the four fundamental mathematical operations, along with addition, subtraction, and multiplication, is division. Division is the process of dividing a larger group into smaller groups so that each group contains an equal number of things. It is a mathematical operation used for equal distribution and equal grouping.
Given:
We have to divide 25 by 12.
The division is as follow:
12| 25 | 2
24
______
1
Thus the Quotient is 2 and remainder is 1.
Learn more about Division here:
brainly.com/question/21416852
#SPJ5
For a given arithmetic sequence, the 75th term, a75, is equal to 342, and the 4th term, 24, is equal to - 13.
nd
Find the value of the 32
term, 232
Answers
Answer:
The 32th term is 127.
Step-by-step explanation:
Arithmetic sequence:
In an arithmetic sequence, the difference between consecutive terms is always the same. The general equation for an arithmetic sequence is given by:
[tex]a_n = a_1 + (n-1)d[/tex]
In which d is the common difference.
It can also be written as:
[tex]a_n = a_m + (n - m)d[/tex]
75th term is equal to 342, and the 4th term, 24, is equal to - 13.
This means that [tex]a_4 = -13, a_75 = 342[/tex]. We use this to find d. So
[tex]a_{75} = a_4 + (75 - 4)d[/tex]
[tex]342 = -13 + 71d[/tex]
[tex]71d = 355[/tex]
[tex]d = \frac{355}{71}[/tex]
[tex]d = 5[/tex]
Find the value of the 32th term:
[tex]a_n = a_m + (n - m)d[/tex]
[tex]a_{32} = a_{4} + (32 - 4)d[/tex]
[tex]a_{32} = -13 + 28(5) = -13 + 140 = 127[/tex]
The 32th term is 127.
Find the area under the standard normal curve that lies outside the interval between z = -2.16 and z = 2.14
Answers
Answer:
The area is 0.0316
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the zscore of a measure X is given by:
[tex]Z = \frac{X - \mu}{\sigma}[/tex]
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X
Find the area under the standard normal curve that lies outside the interval between z = -2.16 and z = 2.14
Below z = -2.16 or Above z = 2.14
Below z = -2.16
z = -2.16 has a pvalue of 0.0154, which means that this area is 0.0154
Above z = 2.14
z = 2.14 has a pvalue of 0.9838, which means that this area is 1 - 0.9838 = 0.0162
Total:
0.0154 + 0.0162 = 0.0316
The area is 0.0316
what is 1235X76678 what is it
Answers
Answer:
94697330
Ur welcome
Step-by-step explanation:
Answer:
94,697,330
Explanation:
[tex]1235 x 76678 = 94697330[/tex]
what is 29x56
if u scam me out of points mad ω
Answers
Answer:
29 x 56 = 1,624
Step-by-step explanation:
5234 ÷ 32 =
y sobran
Answers
Answer:
163.5625 or 163.56
Step-by-step explanation:
Answer:
163.5625
Step-by-step explanation:
2x + 4 < 10 I really need help on this
Answers
Answer:
x < 3
Step-by-step explanation:
Answer:
x < 3
Step-by-step explanation:
treat the sign as if it was an equal sign
then you would solve for x
2x < 6
x < 3
however, there are some cases where the sign would switch directions, you can search up "inequalities algebra" to see more examples
The number of calories in a one ounce serving of a certain chicken sandwich is a random variable with mean 110 calories. The number of calories in a full cup of lemonade is a random variable with mean 140 calories. For lunch, you eat one ounce of the chicken sandwich and LaTeX: \frac{1}{2}1 2 cup of lemonade. Let K be the random variable that represents the total number of calories in this lunch. The mean of K is
Answers
Answer:
The mean of K is 180 calories.
Step-by-step explanation:
Mean of a sum of normal distribution:
The mean of a sum of normal distributions is the sums of the mean.
In this question:
Lunch:
One ounce of chicken sandwich, with mean 110 calories.
Half a cup of lemonade, with mean 140/2 = 70 calories.
Let K be the random variable that represents the total number of calories in this lunch. The mean of K is
110 + 70 = 180 calories
The mean of K is 180 calories.
All of the following monomials are factors of 24x^3z^2–6x^4z^3+12x^2z except:
F. x^2z
G. 3
H. 3x^2z
J. 4xz
K. 6xz
Answers
Answer:
G
Step-by-step explanation:
Ted invests $6,082 in a retirement account with a fixed annual interest rate of 5% compounded continuously. What will the account balance be after 13 years?
Answers
Answer:
$11468.52
Step-by-step explanation:
Given data
Principal= $6,082
Rate= 5%
time= 13 years
The expression for compound interest is
A= P(1+r)^t
substitute
A=6082(1+0.05)^13
A=6082(1.05)^13
A=6082*1.885649
A=11468.52
Hence the Amount is $11468.52
What is the distance from the origin to point P graphed on the complex plane below?
Answers
Answer:
hereeeeeeeeeeee
A $240.00 item is marked down by 25%.
What is the new cost of the item?
Round to two decimals if needed.
$
Answers
Explanation:
240 X 0.25 = 60
240 - 60 = 180
what is the arc of a semicircle with a diameter of 8?
Answers
Step-by-step explanation:
88/7 units
Leslie wants to build a 1,200 piece jigsaw puzzle. The completed puzzle will be in the shape of a rectangle that is 40 pieces in length by 30 pieces in width. Each piece is a square with an area of 0.25 in2. If Leslie wants to build the puzzle on a table that is at least 6 inches larger on all four sides than the complete puzzle, so that it makes a 6-inch border around the puzzle, what are the minimum dimensions of the table that she will need?
Answers
Answer:
If the area of each square piece is 0.25 in, that means that the dimensions must be 0.5 in by 0.5 in. Because the puzzle is 40 pieces by 30 pieces, that gives dimensions of 20 in by 15 in. Adding 6 inches on all four sides of the puzzle, we will have 32 in by 27 in for our minimum table dimensions.
Step-by-step explanation:
If the area of each square piece is 0.25 in, that means that the dimensions must be 0.5 in by 0.5 in. Because the puzzle is 40 pieces by 30 pieces, that gives dimensions of 20 in by 15 in. Adding 6 inches on all four sides of the puzzle, we will have 32 in by 27 in for our minimum table dimensions.
You deposit $400 in an account. The account earns $72 simple interest in 6 years. What is the annual
interest rate?
Answers
The principal was $600.
Explanation:
Find principal by using the formula , where I is interest, P is total principal, i is rate of interest per year, and t is total time in years.
In this example I = $72, i = 4% and t = 3 years, so
Answer: 173,200
Step-by-step explanation:
This is very simple and I can help with this!!
Interest= Principal x Rate x Time
Interest = ($400)($72)(6)= 172,800+400= 173,200
R1 Homework EXTRA CREDIT
R.7-1.1
A set of seven hockey sticks costs $196. What is the cost of one hockey stick?
Answers
Answer:
28
Step-by-step explanation:
7x=196
divide by 7
x=28
Answer:
28
Step-by-step explanation:
7x=196
divide by 7
X = 28
What is the slope of the line?
Answers
Answer:
Slope: -1
Step-by-step explanation:
(0, -2) and (1, -3)
m= (y2-y1)/(x2-x1)
m= (-3+2)/(1-0)
m= (-1)/(1)
m = -1
Kacey is making a bracelet that is 8 inches long. She uses 1 green bead at each end of the bracelet. She also uses 1 green bead every 2 inches
between the two ends. How many green beads does she use?
A. 16
B. 7
C.5
D.4
Answers
Answer:
The answer would be C. 5
Step-by-step explanation:
An exponential distribution is formed by the waiting times for a patient in the emergency room. The average waiting time for this distribution is 38 minutes. Given that it has already taken 37 minutes, what is the probability that the wait time will be more than an additional 41 minutes? Round your answer to three decimal places.
Answers
Answer:
0.207 = 20.7% probability that the wait time will be more than an additional 41 minutes
Step-by-step explanation:
To solve this question, we should understand the exponential distribution and conditional probability.
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
[tex]f(x) = \mu e^{-\mu x}[/tex]
In which [tex]\mu = \frac{1}{m}[/tex] is the decay parameter.
The probability that x is lower or equal to a is given by:
[tex]P(X \leq x) = \int\limits^a_0 {f(x)} \, dx[/tex]
Which has the following solution:
[tex]P(X \leq x) = 1 - e^{-\mu x}[/tex]
The probability of finding a value higher than x is:
[tex]P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^{-\mu x}) = e^{-\mu x}[/tex]
Conditional Probability
We use the conditional probability formula to solve this question. It is
[tex]P(B|A) = \frac{P(A \cap B)}{P(A)}[/tex]
In which
P(B|A) is the probability of event B happening, given that A happened.
[tex]P(A \cap B)[/tex] is the probability of both A and B happening.
P(A) is the probability of A happening.
The average waiting time for this distribution is 38 minutes.
This means that [tex]m = 38, \mu = \frac{1}{38} = 0.0263[/tex]
Given that it has already taken 37 minutes, what is the probability that the wait time will be more than an additional 41 minutes?
Event A: Taking more than 37 minutes.
Event B: More than 37 + 41 = 78 minutes.
Probability of taking more than 37 minutes:
[tex]P(A) = P(X \leq 37) = 1 - e^{-0.0263*37} = 0.6221[/tex]
More than 37 minutes and more than 78 minutes:
The intersection is more than 78 minutes, so:
[tex]P(A \cap B) = P(X > 78) = e^{-0.0263*78} = 0.1286[/tex]
The probability is:
[tex]P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.1286}{0.6221} = 0.207[/tex]
0.207 = 20.7% probability that the wait time will be more than an additional 41 minutes
Help please, just guess and you will be reported show your work.
Answers
Answer:
triangle and conceit is the total and correct
If f (x) = x – 1 and g(x) = 5x – 2 , then (f/g) (x) help me plz
Answers
Answer:
[tex](f/g)x = \frac{x-1}{5x - 2}[/tex]
Step-by-step explanation:
Given
[tex]f(x) = x - 1[/tex]
[tex]g(x) = 5x - 2[/tex]
Required
(f/g)x
In functions:
[tex](f/g)x = \frac{f(x)}{g(x)}\ \ \ g(x)\ne 0[/tex]
So:
[tex](f/g)x = \frac{x - 1}{5x - 2}[/tex]
Which of the following are statistical questions? How many text messages did you send today? What are the ages of the students in Mark’s school? How many days are in a year? How many teeth does Fred have in his mouth? A. Only IV B. Only II C. Only III D. Only I
Answers
Answer:
Only 2
Step-by-step explanation:
2 2/3 divided by 1/3?
Answers
8/3 / 1/3 = 8/3 x 3/1 = 8/1 = 8
Answer:
8
Step-by-step explanation:
i dont know set by step but m brother give me the answer he is in high school
Find the equation of the line parallel to y=6 that contains the point (-1,1). Write the equation in slope intercept form
Answers
Given:
The equation of parallel line is [tex]y=6[/tex].
The line contains the point (-1,1).
To find:
The equation of the line.
Solution:
The slope intercept form of a line is:
[tex]y=mx+b[/tex]
Where, m is the slope and b is the y-intercept.
The equation of parallel line is
[tex]y=6[/tex]
It can be written as
[tex]y=(0)x+6[/tex]
The slope of this line is 0.
The slopes of two parallel lines are always equal. So, the slope of the required line is also 0. It passes through the point (-1,1) so the equation of the line is:
[tex]y-y_1=m(x-x_1)[/tex]
[tex]y-1=0(x-(-1))[/tex]
[tex]y-1=0[/tex]
[tex]y=1[/tex]
Therefore, the equation of the required line is 1.
Wright et al. [A-2] used the 1999-2000 National Health and Nutrition Examination Survey(NHANES) to estimate dietary intake of 10 key nutrients. One of those nutrients was calcium (mg). They found in all adults 60 years or older a mean daily calcium intake of 721 mg with a standard deviation of 454. Using these values for the mean and standard deviation for the U.S. population, find and interpret the probability that a random sample of size 50 will a mean:
Answers
Complete question :
Wright et al. [A-2] used the 1999-2000 National Health and Nutrition Examination Survey NHANES) to estimate dietary intake of 10 key nutrients. One of those nutrients was calcium in all adults 60 years or older a mean daily calcium intake of 721 mg with a standard deviation of 454. Usin these values for the mean and standard deviation for the U.S. population, find the probability that a randonm sample of size 50 will have a mean: (mg). They found a) Greater than 800 mg b) Less than 700 mg. c) Between 700 and 850 mg.
Answer:
0.10935
0.3718
0.9778
0.606
Step-by-step explanation:
μ = 721 ; σ = 454 ; n = 50
P(x > 800)
Zscore = (x - μ) / σ/sqrt(n)
P(x > 800) = (800 - 721) ÷ 454/sqrt(50)
P(x > 800) = 79 / 64.205295
P(x > 800) = 1.23
P(Z > 1.23) = 0.10935
2.)
Less than 700
P(x < 700) = (700 - 721) ÷ 454/sqrt(50)
P(x < 700) = - 21/ 64.205295
P(x < 700) = - 0.327
P(Z < - 0.327) = 0.3718
Between 700 and 850
P(x < 850) = (850 - 721) ÷ 454/sqrt(50)
P(x < 850) = 129/ 64.205295
P(x < 700) = 2.01
P(Z < 2.01) = 0.9778
P(x < 850) - P(x < 700) =
P(Z < 2.01) - P(Z < - 0.327)
0.9778 - 0.3718
= 0.606